Searching Dalam Algoritma Pemrograman C++

POLITEKNIK NEGERI TANAH LAUT

SEARCHING

TI Politala Algoritma Pemrograman 2B

Pengertian Searching

     Algoritma pencarian (Searching algorithm) adalah algoritma yang menerima sebuah argumen kunci dan dengan langkah-langkah tertentu akan mencari argumen kunci tersebut pada data yang telah dimiliki. Setelah proses pencarian dilaksanakan, akan diperoleh salah satu dari dua kemungkinan, yaitu data yang dicari ditemukan (successful) atau tidak ditemukan (unsuccessful).      Ada dua macam teknik pencarian yaitu pencarian sekuensial (sequential search) dan pencarian biner (binary search). Perbedaan dari dua teknik ini terletak pada keadaan data. Pencarian sekuensial digunakan apabila data dalam keadaan acak atau tidak terurut. Sebaliknya, pencarian biner digunakan pada data yang sudah dalam keadaan urut.

Deklarasi Searching

1.   Sequential Search (Linier Search)

    Pencarian Sekuensial (sequential Searching) atau pencarian berurutan sering disebut pencarian linear merupakan metode pencarian yang paling sederhana. Pencarian beruntun adalah proses membandingkan setiap elemen larik satu persatu secara beruntun, mulai dari elemen pertama sampai elemen yang dicari ditemukan atau seluruh elemen sudah diperiksa.

     Teknik pencarian data dari array yang paling mudah adalah dengan cara sequential search, dimana data dalam array dibaca 1 demi satu, diurutkan dari indeks terkecil ke indeks terbesar, maupun sebaliknya. Jika data yang dicari mempunyai nilai yang sama dengan data yang ada dalam kelompok data, berarti data telah ditemukan. Tetapi jika data yang dicari tidak ada yang cocok dengan data-data dalam sekelompok data, berarti data tersebut tidak ada dalam sekelompok data. 

Contoh :

Array :

int A[] = {1,2,3,4,5,6,7,8,9,10} (indeks array pada bahasa C++ dimulai dari indeks ke 0) jika kita ingin mencari bilangan 6 dalam array tersebut, maka proses yang terjadi kita mencari

a)   Dari array indeks ke-0, yaitu 1, dicocokan dengan bilangan yang akan dicari, jika tidak sama, maka mencari ke indeks berikutnya

b)   Pada array indeks ke-1, juga bukan bilangan yang dicari, maka kita mencari lagi pada indeks berikutnya

c)  Pada array indeks ke-2, ternyata bilangan yang kita cari ada ditemukan, maka kita keluar dari looping pencarian.

Contoh program sequential search (Linier Search) :

#include <iostream>

#include <conio.h>

using namespace std;

int main()

{

int A[]={1,2,3,4,5,6,7,8,9,10};

int i, ketemu = 0, n;

int cari;

n = sizeof(A)/sizeof(A[0]);

cout<<"Masukkan data yang dicari : ";cin>>cari;

       for(i=0; i<n;i++)

       {

          if (A[i]==cari)

          {

              ketemu=!ketemu;

              break;

          }

      }

       if(ketemu>0)

       {

            cout<<"Data ditemukan di posisi: "<<i+1;

        }

        else

       {

            cout<<"Data tidak ditemukan";

        }

       getch();

}

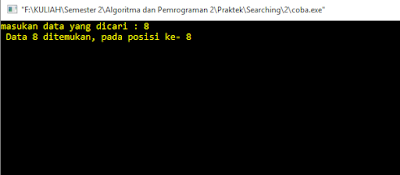
Hasil running :

2.  Binary Search

    Binary search merupakan salah satu algoritma untuk melalukan pencarian pada array yang sudah terurut. Jika kita tidak mengetahui informasi bagaimana integer dalam array, maka penggunaan binary search akan menjadi tidak efisien, kita harus melakukan sorting terlebih dahulu atau menggunakan metode lain yaitu linear search. Namun jika kita telah mengetahui integer dalam array terorganisasi baik secara menaik atau menurun, maka bisa dengan cepat menggunakan algoritma binary search. Adapun ide dasar binary search yaitu memulai pencarian dengan membagi dua ruang pencarian. Misalnya kita memiliki array A, dan kita ingin menemukan lokasi dari spesifik target integer K dalam array. Ada 3 kemungkinan kondisi pada binary search yaitu:

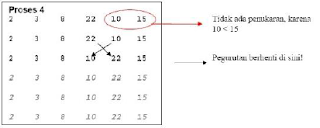
1.   Jika data target K langsung di temukan, maka proses pembagian ruangan berhenti. Kemudian print out indeks data elemen pada array.

2.    Jika data target K < A[middle], maka pencarian dapat dibatasi hanya dengan melakukan pencarian pada sisi kiri array dari A[middle]. Seluruh elemen yang berada di sebelah kanan dapat di abaikan.

3.    Jika data target K > A[middle], maka akan lebih cepat jika pencarian di batasi hanya pada bagian sebelah kanan saja.

4.    Jika seluruh data telah di cari namun tidak ada, maka diberi nilai seperti -1.

Dibawah ini merupakan salah satu versi program binary search :

#include <iostream>

#include <conio.h>

using namespace std;

int main()

{

      const int Ar[10] = {1,2,3,4,5,6,7,8,9,10}; // untuk proses ascending

      int tar;

      cout<<"masukan data yang dicari : "; cin>>tar;

      int awal=0, akhir=10, tengah;

      while (awal <= akhir)

     {

             tengah = (awal + akhir)/2;

             if (tar > Ar[tengah] )   // descending ubah tanda > menjadi <

            {

                   awal = tengah + 1;

 }

             else if (tar < Ar[tengah]) // descending ubah tanda < menjadi >

            {

       akhir= tengah - 1;

}

            else

{

       awal = akhir +1;

            }

      }

      if (tar == Ar[tengah])

     {

cout<<" Data "<<tar<<" ditemukan, pada posisi ke- "<<tengah+1<<endl;

      }

      else

     {

cout<<"Data "<<tar<<" tidak ditemukan "<<endl;

  }

  getch();

}

Hasil running :

Contoh Program Binary Search Lainnya

 Hasil running :

Jika ingin contoh program searching yang lainnya, silahkan download pada link :

https://drive.google.com/file/d/1GYikXGDSaHZEJLr4ED2ZTbSweU20LHtI/view?usp=sharing
https://drive.google.com/file/d/1nk8u6DORb81BFy0ohTf4oU17MB_oJ1Zu/view?usp=sharing
https://drive.google.com/file/d/1RZx7slXN0wNBEXg-YuT0Y98CUR6qHREq/view?usp=sharing
https://drive.google.com/file/d/1m1MpQrSBRN3A5INrXEQGbVB7IAXDo22Q/view?usp=sharing

https://drive.google.com/file/d/1xd8MIMquMMkSsJ6BxomDbE73mLLL3EX_/view?usp=sharing

DAFTAR PUSTAKA

Muhidin, Asep. 2010. Modul Kuliah Pemrograman Bahasa C++, Bekasi; Penerbit Zeyrank Offset.

Arhami, Muhammad. 2010. “MODUL PRAKTIKUM ALGORITMA DAN STRUKTUR DATA”. Pendidikan Teknik Informatika. Politeknik Universitas Negeri Malang.

Rahmaddeni. 2012. “ANALISA PERBANDINGAN ALGORITMA PENCARIAN (SEARCHING ALGORITM)”. Jurnal. Jurnal Sains dan Teknologi Informasi, Vol. 1, No. 1.

Read more...

Sorting Dalam Algoritma Pemrograman C++

POLITEKNIK NEGERI TANAH LAUT

SORTING

TI Politala Algoritma Pemrograman 2B

Pengertian Sorting

Sorting adalah proses mengatur sekumpulan objek menurut aturan atau susunan tertentu. Urutan objek tersebut dapat menaik atau disebut juga ascending (dari data kecil ke data lebih besar) ataupun menurun/descending(dari data besar ke data kecil).

Metode Sorting :

1. Bubble Sort (Metode Gelembung)
2. Quick Sort atau Exchange Sort
3. Merge Sort (Metode Penggabungan)
4. Shell Sort 
5. Insertion Sort (Metode Penyisipan)
6. Selection Sort (Metode Seleksi)

Disini saya hanya akan membahas 3 metode yaitu Bubble Sort (Metode Gelembung),  Guick Sort atau Exchange Sort, dan Marge Sort (Metode Penggabungan).

Jenis-Jenis Metode Sorting

1.   Bubble Sort

      Merupakan metode sorting termudah, diberi nama “Bubble” karena proses pengurutan secara berangsur-angsur bergerak/berpindah ke posisinya yang tepat, seperti gelembung yang keluar dari sebuah gelas bersoda. Bubble Sort mengurutkan data dengan cara membandingkan elemen sekarang dengan elemen berikutnya. Jika elemen sekarang lebih besar dari elemen berikutnya maka kedua elemen tersebut ditukar, jika pengurutan ascending. Jika elemen sekarang lebih kecil dari elemen berikutnya, maka kedua elemen tersebut ditukar, jika pengurutan descending. Algoritma ini seolah-olah menggeser satu per satu elemen dari kanan ke kiri atau kiri ke kanan, tergantung jenis pengurutannya. Ketika satu proses telah selesai, maka bubble sort akan mengulangi proses, demikian seterusnya. Kapan berhentinya? Bubble sort berhenti jika seluruh array telah diperiksa dan tidak ada pertukaran lagi yang bisa dilakukan, serta tercapai perurutan yang telah diinginkan.

Pada gambar di atas, pengecekan dimulai dari data yang paling akhir, kemudian dibandingkan dengan data di depannya, jika data di depannya lebih besar maka akan ditukar.

Pada proses ke-2, pengecekan dilakukan sampai dengan data ke-2 karena data pertama pasting sudah paling kecil.

Untuk contoh program ini adalah

#include <iostream>
#include <conio.h>
using namespace std;
main()
{
     int nilai['n'];
     int temp;
     int n;
     cout<<"Banyak Data: "; cin>>n;
     cout<<endl;
     for (int a=1; a<=n; a++)
    {
         cout<<"nilai[“<<a<<“]: "; cin>>nilai[a];
    }
    cout<<"\n\n";
    cout<<"Data Sebelum diurutkan"<<endl;
    for(int a=1; a<=n; a++)
    {
         cout<<nilai[a]<<" ";
    }
    for(int a=n-1; a>=1; a--)
   {
        for(int b=1; b<=a; b++)
        {
              if(nilai[b]>nilai[b+1])
              {
                   temp=nilai[b+1];
                   nilai[b+1]=nilai[b];
                   nilai[b]=temp;
               }
          }
    }
    cout<<"\n\nData Setelah Diurutkan (Ascending)"<<endl;
    for (int a=1; a<=n; a++)
   {
        cout<<nilai[a]<<" ";
   }
   cout<<"\n\n";
   cout<<"\n\nData Setelah Diurutkan (Descending)"<<endl;
   for (int a=n; a>=1; a--)
   {
         cout<<nilai[a]<<" ";
   }
   getch();
}
Hasil Running :

2.   Quick Sort atau Exchange Sort

     Quick Sort merupakan suatu algoritma pengurutan data yang menggunakan teknik pemecahan data menjadi partisi-partisi, sehingga metode ini disebut juga dengan nama partition exchange sort. Untuk memulai irterasi pengurutan, pertama-tama sebuah elemen dipilih dari data,  kemudian elemen-elemen data akan diurutkan diatur sedemikian rupa. Metode Quick sering disebut juga metode partisi (partition exchange sort). Metode ini mempunyai efektifitas yang tinggi dengan teknik menukarkan dua elemen dengan jarak yang cukup besar. Metode pengurutan quick sort dapat diimplementasikan dalam bentuk non rekursif dan rekursif. Berbagai varian dari quicksort pada intinya berupaya untuk mengembangkan teknik-teknik pembuatan partisi yang efektif untuk berbagai macam masukan.Hal ini merupakan bahan yang terus dipelajari hingga kini.Ditambah pula dengan perbaikan dari segi pemrograman sehingga lebih efisien (seperti mengurangi operasi pembandingan, pertukaran maupun perulangan).

     Sangat mirip dengan Bubble Sort, dan banyak yang mengatakan Bubble Sort sama dengan Exchange Sort. Perbedaan ada dalam hal bagaimana membandingkan antar elemen-elemennya. Exchange sort membandingkan suatu elemen dengan elemen-elemen lainnya dalam array tersebut, dan melakukan pertukaran elemen jika perlu. Jadi ada elemen yang selalu menjadi elemen pusat (pivot). Sedangkan Bubble Sort akan membandingkan elemen pertama/terakhir dengan elemen sebelumnya/sesudahnya, kemudian elemen sebelum/sesudahnya itu akan menjadi pusat (pivot) untuk dibandingkan dengan elemen sebelumnya/sesudahnya lagi, begitu seterusnya.

untuk contoh program ini adalah

#include <iostream>
#include <conio.h>
using namespace std;
void tampilkan_data(int data[], int n)
{
     int i;
     for (i=1;i<=n;i++)
     cout<<data[i]<<" ";
     cout<<"\n";
}
int partisi (int data[], int awal, int akhir)
{
      int x,i,j,simpan;
      //www.nutekno.com
      i=awal;
      j=akhir;
while(1)
{
    while(data[i]<data[awal])
    i=i+1;
    while(data[j]>data[awal])
     j=j-1;
    if (i<j)
    {
        //tukarkan data
        simpan=data[i];
        data[i]=data[j];
        data[j]=simpan;
    }
   else
      return j;
   }
}
void quick_sort(int data[], int awal, int akhir)
{
      int q;
      if(awal<akhir)
   {
        q=partisi(data,awal,akhir);
        quick_sort(data,awal,q);
        quick_sort(data, q+1,akhir);
    }
}
int main()
{
    int i,j,n,data[100];
    cout<<"masukkan banyak data= ";cin>>n;
    for(i=1;i<=n;i++)
   {
         cout<<"data ke-"<<i<<" = ";cin>>data[i];
   }
   cout<<"Data sebelum diurut: "<<endl;
   for(j=1;j<=n;j++)
  {
       cout<<data[j]<<" ";
   }
   quick_sort(data,1,n);
    //hasil pengurutan
    cout<<endl<<endl;
    cout<<"hasil pengurutan:\n";
    tampilkan_data(data,n);
 getch();
}
Hasil Running :

3.   Merge Sort

Merge sort adalah algoritme divide-and-conquer berdasar kepada proses memecah list menjadi beberapa sublist hingga pada akhirnya tiap sublist hanya berisi satu elemen lalu sublist tersebut akan digabungkan dengan cara tertentu hingga list tersortir.

Konsep Dasar:

• Membagi list acak menjadi NN sublist, masing-masing memiliki 11elemen.
• Ambil sepasang list singleton dan gabungkan mereka menjadi list dengan 2 elemen. NN akan dikonversi menjadi N/2N/2 list dengan ukuran 2.
• Ulangi proses ini hingga tersisa satu list yang sudah teratur.

Saat membandingkan dua sublist untuk digabungkan, elemen pertama pada kedua list akan dijadikan dasar pertimbangan. Saat melakukan penyortiran dengan urutan ascending, elemen dengan nilai yang lebih kecil akan menjadi elemen baru dari list tersortir. Prosedur ini diulangi hingga sublist yang lebih kecil kosong dan sublist hasil penggabungan baru memiliki semua elemen kedua sublist.

Sebagaimana yang dapat dipahami dari gambar di atas, pada setiap langkah, list dengan ukuran MM dibagi menjadi 22 sublist berukuran M/2M/2, hingga pembagian tidak dapat lagi dilakukan. Lebih mudahnya, diketahui terdapat array AA yang lebih kecil dengan elemen (9,7,8)(9,7,8).

Pada langkah pertama, list berukuran 33 dibagi menjadi 22 sublist dengan sublist pertama terdiri dari (9,7)(9,7) dan sublist kedua terdiri dari (8)(8). Sekarang, list pertama yang terdiri dari elemen (9,7)(9,7)dibagi lagi menjadi 22 sublist terdiri dari elemen (9)(9) dan (7)(7) secara berurutan.

Sublist tersebut tidak dapat dibagi lagi karena setiap sublist hanya memiliki 11 elemen, kini kita akan mulai menggabungkan list tersebut. 22 sublist yang terbentuk pada langkah terakhir akan digabungkan sesuai urutan menggunakan prosedur yang disebutkan di atas dan membentuk list baru (7,9)(7,9). Dengan melakukan backtracking, kita akan menggabungkan list yang berisi elemen (8)(8)dengan list ini, sehingga list baru yang tersortir terbentuk (7,8,9)(7,8,9).

Implementasi cara tersebut tersedia di bawah ini:

void merge(int A[ ] , int start, int mid, int end) 
{

    //menyimpan posisi awal kedua posisi awal kedua bagian dalam variabel temporer

    int p = start ,q = mid+1;

    int Arr[end-start+1] , k=0;

for(int i = start ;i &lt;= end ;i++)

{

     if(p &gt; mid)      //memeriksa apabila bagian pertama berakhir atau belum

     Arr[ k++ ] = A[ q++] ;

     else if ( q &gt; end)   //memeriksa apabila bagian kedua berakhir atau belum

     Arr[ k++ ] = A[ p++ ];

     else if( A[ p ] &lt; A[ q ])     //memeriksa bagian mana yang memiliki elemen yang lebih kecil

     Arr[ k++ ] = A[ p++ ];

     else

     Arr[ k++ ] = A[ q++];

 }

for (int p=0 ; p&lt; k ;p ++) 

{

    /* Sekarang array yang sebenarnya memiliki elemen yang tersortir untuk kedua bagian. */

    A[ start++ ] = Arr[ p ] ;                         

}
}

Di sini, pada fungsi merge, kita akan melakukan merge pada dua bagian array di mana satu bagian memiliki posisi dari awal hingga pertengahan dan bagian lain memiliki posisi mid+1 hingga akhir.

Awalan diambil dari bagian depan array, yaitu p dan q. Lalu elemen pada kedua bagian akan dibandingkan dan elemen dengan nilai yang lebih kecil akan disimpan di auxiliary array (Arr[ ]). Jika pada kondisi tertentu, salah satu bagian berakhir, maka semua elemen dari elemen yang satunya akan ditambahkan ke auxiliary array dengan urutan yang sama.

Amati 2 fungsi recursion bercabang berikut ini:

void merge_sort (int A[ ] , int start , int end )

{

     if( start &lt; end ) 

     {

           int mid = (start + end ) / 2 ;    // membagi array menjadi dua bagian

           merge_sort (A, start , mid ) ;  // menyortir bagian pertama array

           merge_sort (A,mid+1 , end ) ;// menyortir bagian kedua array

           // menyatukan kedua bagian dengan membandingkan elemen pada kedua bagian

          merge(A,start , mid , end );  

      }                   

}
untuk contoh program ini adalah
#include <iostream>
#include <conio.h>
using namespace std;
int a[50];
void merge(int,int,int);
void merge_sort(int low,int high)
{
     int mid;
     if(low<high)
     {
          mid=(low+high)/2;
          merge_sort(low,mid);
          merge_sort(mid+1,high);
          merge(low,mid,high);
     }
}
void merge(int low,int mid,int high)
{
     int h,i,j,b[50],k;
     h=low;
     i=low;
     j=mid+1;
    while((h<=mid)&&(j<=high))
    {
         if(a[h]<=a[j])
         {
              b[i]=a[h]; h++;
          }
         else
         {
              b[i]=a[j]; j++;
          } i++;
     }
 if(h>mid)
 {
       for(k=j;k<=high;k++)
       {
            b[i]=a[k]; i++;
        }
  }
        else
       {
             for(k=h;k<=mid;k++)
             {
                  b[i]=a[k]; i++;
              }
        }
              for(k=low;k<=high;k++)
              a[k]=b[k];
        }
main()
{
 int num,i;
 cout<<"*******************************************************************"<<endl;
 cout<<"                         MERGE SORT PROGRAM "<<endl;
 cout<<"*******************************************************************"<<endl;
 cout<<endl<<endl;
 cout<<"Masukkan Banyak Bilangan : ";cin>>num;
   cout<<endl;
 cout<<"Sekarang masukkan "<< num <<" Bilangan yang ingin Diurutkan :"<<endl;
 for(i=1;i<=num;i++)
 {
  cout<<"Bilangan ke-"<<i<<" : ";cin>>a[i] ;
 }
 merge_sort(1,num);
 cout<<endl;
 cout<<"Hasil akhir pengurutan : "<<endl;
 cout<<endl;
 for(i=1;i<=num;i++)
  cout<<a[i]<<" ";
 cout<<endl<<endl<<endl<<endl;
   getch();

}

Hasil Running :

DAFTAR PUSTAKA

https://indonesia.hackerearth.com/merge-sort/

http://yuliana.lecturer.pens.ac.id/Struktur%20Data/TEORI/T7%20-%20Quick%20dan%20Merge%20Sort.pdf https://muhammadhaluanrangkuti.blogspot.com/2016/10/pengertian-dan-metode-quick-sort.html

Read more...